If you are bullish on a given underlying, you probably think about buying a naked call. However, sometimes, the only option available to buy is a put. Should you buy it? Short answer: YES.
However, to replicate the call payoff, you actually need to delta hedge the put and then buy even more shares, to an amount equivalent to 100 delta... Which means that if you buy 1000 puts, then you buy 1000 shares.
To illustrate: If the call you wanted to buy initially has a 40 delta, then put at the same strike will have a 60 delta (put/call parity...) To equate the 40 delta of the call, then buy 40 delta more worth of shares... As simple as that.
Then, once the position is in place, if the the combination of put + shares will replicate a position on the naked call:
- when the underlying moves higher
- the put delta value will decrease, as well as the delta of the option (at a decreasing rate)
- the long shares position will gain in value
- when the underlying moves lower
- the put value will increase, as well as the delta
- the long shares position will lose money
The greeks profile in terms of gamma, theta and volatility will be the same.
Differences will arise if the option is american and there are dividends as the put is never exercised, while a deeply in the money call will be exercised before the dividend ex-date.
Below, using a Black Sholes pricer, comparison between the values of a 3month 50 naked call with a 50 spot price, volatility = 25% and an equivalent put, over-hedge (according to the description above) with respect to spot price changes.
And voila, under your eyes, you can see that we have a replicating portfolio.
Showing posts with label Derivatives trading. Show all posts
Showing posts with label Derivatives trading. Show all posts
Monday, 22 October 2012
Saturday, 8 September 2012
Steepness in the Forward Volatility Term Structure
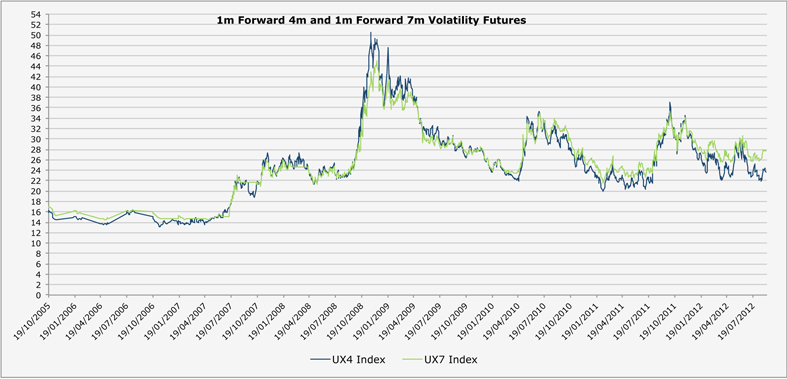
I was looking at the steepness in the forward implied volatility and found something interesting. Currently, in the wonderful VIX world, the 1 month forward volatility term structure is the steepest ever (99th percentile) over the last 7 years, when looking at the difference between the 7 month and 4 month forward contracts (UX7 Index and UX4 Index in Bloomberg). The difference is 4 vols.
The trade here, is to sell the 7 month and to buy the 4 month contract in order to benefit from the convergence between the two volatilities. So the position is paying decay. In order to figure out how much decay the position is inflicting, I had a look at the 1 month / 3 month contracts spread in order to assess the cost of carry. The difference is 5 vols, which means that, provided we hold the position until maturity, the cost of holding the spread is 1 vol.
Looking at the risk/reward, I believe that the maximum steepness between the two contracts will be 5 to 6 vols (losing 1 to 2), while the possible gain is of 4 to 6 vols. the risk/reward ratio seems appealing, while the cost of carrying the positing is one of the smallest since 2005.
Why is the forward term structure so steep?
I think that at the moment, we are in a world of financial repression where equity and bond markets are wherever central banks want them to be. The greater the level of monetary expansion, the calmer the VIX and the higher the gains in the S&P Index.
So, as realised volatility is poor and the equity market is rallying, implied volatilities are drifting lower and lower (even to truly absurd levels given the state of our economies), especially in the front end of the term structure. However, market participants still expect volatility to pick up in the future.
So in a certain way, we go back to the same question, which is how long our politicians and central bankers can kick the can down the road and avoid confronting the real issues.
Looking at the risk/reward, I believe that the maximum steepness between the two contracts will be 5 to 6 vols (losing 1 to 2), while the possible gain is of 4 to 6 vols. the risk/reward ratio seems appealing, while the cost of carrying the positing is one of the smallest since 2005.
Why is the forward term structure so steep?
I think that at the moment, we are in a world of financial repression where equity and bond markets are wherever central banks want them to be. The greater the level of monetary expansion, the calmer the VIX and the higher the gains in the S&P Index.
So, as realised volatility is poor and the equity market is rallying, implied volatilities are drifting lower and lower (even to truly absurd levels given the state of our economies), especially in the front end of the term structure. However, market participants still expect volatility to pick up in the future.
So in a certain way, we go back to the same question, which is how long our politicians and central bankers can kick the can down the road and avoid confronting the real issues.
Labels:
Derivatives,
Derivatives trading,
Forward Volatility,
Forward Volatility Term Structure,
Implied Volatility,
Tail Risk,
VIX,
Volatility trading
Monday, 3 September 2012
Bearish Trading Strategy - with a twist
If you are bearish on an underlying, on low
implied volatility names, you can:
- Buy a
naked put spread
- Buy a
put (hedged)
- Buy
an upside call (hedged)
Let's talk about the last trading strategy. It
sounds counterintuitive, however, let's have a closer look.
The interesting part is that, on a low implied
volatility / high convexity underlying, the return is higher than on a hedged
long put. See the detailed analysis below, for an instantaneous 5% down move.
Notes:
- As
the spot moves down by 5%, implied volatility follows the skew and is
readjusted. Lets imagine (and this is purely fictive) that implied volatility
moves up by 1% (fixed strike). Also, as we move away from our call, its implied
volatility increases more (convexity). So we considered that for the call, the
adjustment is 2 vols (This is an rough estimate - no science behind)
- Being
long the call, we end up with 9% delta, so we are still a bit short shares.
Being long the put creates a larger delta position, so we are more and more
long shares of a crashing underlying.
- The
highest performance is from the put spread strategy, we left it as a benchmark.
Labels:
Bearish Trading Strategy,
Convexity,
Derivatives,
Derivatives trading,
Implied Volatility,
Put Spread
Monday, 27 August 2012
Equity Volatility Skew
Equity Volatility Skew
Equity Volatility Skew, sometimes called strike skew, is the
measure of the disparity of option implied volatility for option contracts with
different strikes but the same expiration. It is the extrapolated tangent
between two given strikes implied volatility, and thus a slope.
In equities, most of
the time, it has a negative slope and is expressed by moneyness as the arithmetic
difference between implied volatility of the 90% put option and the implied volatility
of the 110% call option. It can also be expressed by strike (sticky strike, vol by
constant strikes) or by delta (sticky delta, vol by delta constant).
Skew and Black Scholes
Existence of Strike skew is
not predicted by the Black-Scholes model. Black Scholes model assumes that volatility
is a property of the underlying instrument, so the same implied volatility
value should be observed across
all options on the same instrument.
Equity volatility skew is a consequence of
empirical violations of the black Sholes stock prices return distribution
assumptions. Indeed, the Black-Scholes model assumes that stock prices are
lognormally distributed, which in turn implies that stock log-prices are
normally distributed.
Reasons for a Skew
Empirical: Market returns are more
leptokurtic than assumed in by the lognormal distribution. Market leptokurtosis
would make way out-of-the-money or way in-the-money options more expensive than
would be assumed by the Black-Scholes formulation. So by increasing prices for
such options (and thus implied volatility), existence of implied volatility
skew is a way of achieving higher prices than within the Black-Scholes model.
Statistical: Markets tend to fall
harder than they rise and skewness is a measure of the asymmetry of the distribution.
Being the 3rd standardized moment and representing this asymmetry, skewness
expresses in a certain way the observed correlation between the move of a random
process and its volatility (on this - to assess the risk neutral distribution
asymmetry implied by an option, a theoretical framework or model is needed)
Behavourial: Volatility skew could
reflect investors fear of market crashes, as deeply out of the money puts are a
form of insurance against market crashes. As they are considered as low cost in
terms of dollars, deeply out of the money puts are widely used as a protection
tools. Thus, skew can be seen as the perceived tail risk of the distribution of
the market and can be a valuable indicator that shows the market sentiment
toward a given underlying.
Structural Demand and Supply: The market
is ‘long stock’, so investors naturally tend to sell high strike calls options (to
enhance the yield of the portfolio through income) and to buy puts options in order to
protect the portfolio returns.
Use of the skew:
The first thing is that
there is not a single measure of equity volatility skew that is unambiguously best for all
purposes. In fact, skew is dependent from volatility level, maturity, spot
price. A very interesting way of expressing skew is (25 delta put volatility-25
delta call volatility) / 50 delta volatility, which emerges as the preferred
skew measure based on the theoretical and empirical analysis.
Predictive power of
returns: Academics tend to suggest that there is predictive
information content within the volatility skew, especially in the short-term
for stock market returns. However, market practitioners tend to make no money
from such findings. So it seems that there is no clear empirical relationship... Sorry guys.
There have been many attempts in the
academic literature to model the behavior of changes in skew, but the
interpretation of skew information by traders is still done largely on a
qualitative and ad hoc basis.
Trading
Skew
An experienced trader
explained me a rule of thumb, 10 delta difference between 2 options should
roughly equate to 1 vol difference. Skew will be expensive if above 1.5 and
cheap if below 0.5.
Risk Reversals, Put
Spreads and Call Spreads are skew trading strategies. The main drawbacks when
entering such king of strategy is that realisation of the skew will be impacted
by vol level and spot level, so a decent amount of noise will come affect the
trade. As the trade is done, moneyless/delta of the options is affected by the
spot and/or volatility changes and passage of time.
Also, when trading
short term options (less than 3m, for example) most of skew buying strategies
tend to have poor gamma/theta ratios. In other
words owning gamma via puts with high skews can be expensive in terms of theta
decay compared to a portfolio made up of at-the-money or call options.
Labels:
Derivatives,
Derivatives trading,
Equity Volatility Skew,
Skew,
Tail Risk,
Trading Skew,
Volatility,
Volatility trading
Wednesday, 15 August 2012
Game On (Tail risk in European Equities)
Today, I was wondering how much of tail risk is priced in the market at the moment. EURUSD currency pair provides one of the purest way of trading a potential Euro Zone breakup, while European stocks are my natural
underlying (because of my job).
Tail risk is cheap on a 5 year
relative basis in FX and damn cheap in equities.
- EURUSD: 6M 25D Butterfly:
Currently in 24th percentile on 5Y history
- Eurostoxx 50:
- 6M Put Skew (90%-100%)
currently in 9th percentile on 5Y history
- 6M Call Skew (100%-110%)
currently in 7th percentile on 5Y history
Most of the person I talk to
believe that the probability of a breakup of the euro through exit of Greece is non-negligible. Some of them even consider as pretty much already done. So I have a hard time reconciling the idea of a Euro break up (a true tail risk event, from my view) and low implied
volatility.
Indeed, it is not very clear how a
country can leave (or be forced to leave) the eurozone from a legal and
practical point of view. We have a very interesting paper which won the Wolfson
Prize on this topic, stating that ‘Overall, () analysis has revealed a series
of very tricky issues which any exiting country would need to face” “but all of
these difficulties can be overcome”.
In Summary, a country, such as
Greece, contemplating leaving the euro would have to keep its plans secret
until the last minute, introduce capital controls, start printing a new
currency only after formal exit, implement last-minute bank holidays, seek a
large depreciation (30/50%), default on its debts (note: redomination of debt
may not automatically lead to default as it depends on lex monetae and
contractual intentions, especially for countries that have issued debt under
domestic law), recapitalise bust banks and seek close co-operation with remaining
euro members.
“Such a rebalancing of the economy
away from reliance on net exports would be in the interests of the whole of the
current membership of the eurozone, as well as countries outside it,” according
to the paper. Nice.
Moreover, an exit also means heavy losses
for debt holders as debt is likely to be re-denominated in the depreciated new
currency. One-Off public costs of a euro area exit for European counterparts of
Greece (from The Economist) in Eur would be 323bn:
- Aid package 50bn
- Disbursements in bails
outs 127bn
- Govt bonds held by ECB 40bn
- Target2 debt 106bn
Talking about tail risk, I found an
interesting note by Bank of America-Merrill Lynch on game theory and euro breakup risk premium published
in July12. It explains that an uncooperative outcome dominates the strategies
of both Germany and Greece (this is why we are stuck for the last 2 years).
The paper also explains that in looking at output growth, borrowing cost,
balance sheet impacts, Italy and Ireland are the two countries benefiting most
from a voluntary exit of euro. Germany, despite being the most likely to leave,
has the lowest incentive to do so due to negative impact on growth and loss
from debt holding. So the game of Germany would be to ‘bribe’ Italy to stay.
However, the Nash equilibrium of
the game would be an exit of Italy regardless of what Germany does. This sounds
a bit extreme. However, I try to keep in mind that the world is much more
violent than what we would like to think and outcomes much more volatile than
predicted in our models.
So I do not understand why tail
risk is currently priced so low, if we consider the implications of a euro break up: sorting out the uncertainties and taking the losses.
The only thing I can think about is
QE and/or a weaker Euro… A recent survey of fund managers showed that 80% of
fund managers see ECB doing QE in Q3/Q4. So SX5E Call Spreads are really cheap
then?
References
http://www.economist.com/node/21560252
Labels:
Derivatives trading,
Equity Volatility Skew,
European Crisis,
Tail Risk,
Volatility,
Volatility trading
Tuesday, 14 August 2012
Bloomberg Functions For Equity
Equities Function
WEI World
Equity Indices
HVG Historical
Volatility Graph
HVT Historical
Volatility Table
HCP Historical
Daily changes and Volumes
HVP M Historical
Monthly changes and Volumes
HRH Historical
returns distribution
VAP Traded
prices + VWAP for a given intraday period
DES Company
Description
HDS Company’s
Owners
FA Company’s
Financial Analysis (BS, IS, CFS)
GV Historical
IV and RV Volatility (can chose % Moneyness for IV)
GIV Intraday
implied volatility changes (fixed strike)
OV Option
Pricing (includes payoff and Greeks graphs)
OSA Option
Portfolio (from OV)
OVDV Volatility
surfaces (much better than SKEW function)
OMON Option
Monitor, linked to the exchanges
MOSO Option
Most traded across markets
OMST Option
Most traded for a given underlying
OSCH Option
research tool
CT Contract
table (useful for Futures)
FH Futures
Hedge Ratio
BI Bloomberg
Industries (overview, detailed analysis of an industry)
RV Relative
Value tool (becomes powerful with customisation tools)
G Graph
GIP Intraday
Chart (can type GIP10)
GPC Long
Term Candle Chart
IGPV Graph
with technical studies
CIX Advanced
Graphing tool (spreads, ratios, etc)
HS Historical
Spreads with Statistical analysis
BTST Back
Testing of generic technical trading signals
READ Most
popular News
TOP Top
News
FIRS Bloomberg
First News
NI HOT Hot Headlines
NLRT Set
up News Alert
TNI Search
tool
CN Company
News
Monday, 13 August 2012
Let The Good Times Roll (European Equities and Credit)
The
relationship between stock price volatility and CDS spread is statistically
strong, with a historical correlation close to 0.70 in both regions.
Below, a
comparison of current Volatility and Credit levels
- Volatility is measured as V2X and VIX
- Credit is measured as Markit Itraxx Europe and USA Generic
5Y corporate CDS (basket of 125 cds for each)
Source: Bloomberg
Source: Bloomberg
Today, credit is in 80th percentile and 63rd percentile in Europe and USA, respectively while equity volatility is in the 52nd percentile and 34th percentile. In Europe, the spread is particularly large. This conflicting signal puzzles me, especially if I look at the following items (the list could be long):
-
Still potential breakup of the eurozone, with all the mess
it implies
-
ESM still not in
place and no clear support for a banking license that will allow the entity to
fund itself
-
ECB bond purchases seniority issue not resolved, pushing
private investors down the pecking order of creditors
-
Deterioration of corporate earnings and economic
indicators
From the
other hand, the spread between equity volatility and credit could remain at
high levels
-
The performance of equity markets is not that bad (+5.4%
so far in 2012), served by relatively better yields than in the rates market
and low valuation
-
The CDS index has 25% of financial companies against 22%
for the Equity index, explaining part of the difference
-
Also, CDS has underperformed vs Cash, due to the lack of
liquidity in the cash market and positive basis
As the
answer will come from our politics, so the catalysts to look at in September
are the following:
- 6th Sep : ECB Meeting :
SMP details?
-
12th Sep : Constitutional court of Karlsruhe for ESM vote
-
13th Sep: Fed meeting: QE3 or not QE3?
-
15th Sep : Euro Group meeting
What
history tells us:
From Luc
Laeven and Fabian Valencia, IMF : "An interesting pattern emerges: banking
crises tend to start in the second half of the year, with large September and
December effects."
From
Roggof, Harvard: crises to happen in election years. The intuition behind is
that crises are the result of imbalances that accumulate over a long time.
Politicians have a strong incentive to delay dealing with them until after an
election, and often, as was the case with Greece, to actually hide the truth
until the polls close. We had Elections in France, and US and China leadership
transition on the agenda.
Personally,
I tend to think that August will probably remain quiet.
However, I am really worried
about September 12, Equity
volatility should explode.
So let’s enjoy the end of the summer while it lasts.
Labels:
Credit,
Derivatives,
Derivatives trading,
European Crisis,
Volatility
Subscribe to:
Posts (Atom)